机器人之死——逻辑、直觉和悖论，决策者的困境

老胡说科学  发布时间: 06-01

每隔一段时间，我们就会看到一些关于人工智能（AI）的爆炸性新闻，人工智能是将我们的思维方式自动化的学科。去年，有新闻称“人类不再需要证明数学定理了”，这指的是2019年谷歌的一篇关于使用人工智能证明数学定理的论文。这条新闻意味着人工智能最终将取代数学家。

人工智能取代数学家的想法源于对逻辑的研究，这可以追溯到2500年前的亚里士多德，他认为直觉和逻辑是获得知识的两个方面。然而，在计算机出现之前，逻辑因为其严谨性和确定性而比直觉更受青睐，这使得逻辑推理得以正式研究并最终实现自动化。计算机是2000多年来逻辑推理发展到极致的结果，这最终实现了无需人类思维的自动逻辑推理。然而，事实证明，逻辑推理及其自动化是不够的，因此，直觉对数学来说是不可或缺的。矛盾的是，在我们了解了逻辑推理的极限之后，我们发明了一种新工具——计算机，来利用我们的直觉。从亚里士多德学派试图让数学变得毫无意义，以至于可以由机器来完成，到柏拉图学派想知道机器是否能像我们一样真正理解数学的意义，历史经历了一个轮回。

在人工智能的许多研究领域中，“人工智能取代数学家”实际上是计算机之前的人工智能，它有一个特殊的地位，因为它的失败导致了计算机的发明。回顾现代人工智能如何取代数学家可能会帮助我们找到最后一块拼图，这可以应用于任何形式的知识发展，包括人工智能本身。在人们担心恶意的人工智能会反射出我们的阴暗面之际，看看人工智能能否模仿人类当中最优秀的人：伟大的数学家、科学家和思想家，或许是件令人高兴的事。

如何杀死一个机器人？

在《星际迷航》的一集中，柯克船长（Captain Kirk）遇到了一群流氓机器人，他们击落了宇宙飞船，并计划毁灭全人类，因为他们逻辑上认为人类造成了宇宙的所有问题。为了打败如此强大的敌人，柯克计划使用“狂野而非理性的逻辑”作为强大的武器。最后，机器人的首领诺曼，被其中最疯狂、最不合理的逻辑——说谎者的悖论所毁灭。柯克说马德说的都是谎话，马德对诺曼说，“仔细听着，诺曼。我……在撒谎。”为了解决这个悖论，诺曼抽着烟，自毁了。这样我们就看到了一个机器人的死亡。说谎者的悖论可以如下图所示：

说谎者悖论

悖论来源于“这句话”指的是“这句话”所属的整个句子。如果我们假设这个句子说的是真的，那么这个句子就是假的，因为这就是它说的。这与我们的假设相矛盾。另一方面，如果这个命题说的是假的，那么它说的反面一定是真的，也就是说这个命题是真的，这又是一个矛盾。悖论是逻辑最大的敌人。看看它是如何导致诺曼死亡的。事实上，如果诺曼思考关于自己的问题，他的逻辑大脑会遇到一种自我指向悖论，类似于说谎者的悖论。诺曼隐喻地反映了数学家如何面对自我参照和随之而来的悖论。

亚里士多德：逻辑的力量

亚里士多德，希腊哲学家和博物学家（公元前384-322），是逻辑学之父。他研究了我们如何以正式的方式进行理性思考。他认为逻辑推理独立于可能应用的上下文。例如：

人皆有一死。

苏格拉底是一个人。

因此，苏格拉底终有一死

这是三段论的一个应用，所有A都是B，所有C都是A，因此所有C都是B ，其中A，B和C是变量，可以代表现实中的任何东西。假设前提的真实性，逻辑结果的真实性应该是确定的。然而，如果不陷入无限回归，就没有办法证明前提的真实性。因此，亚里士多德认为“直觉给我们公理”，不言而喻的真理作为起始前提。其余的真理要么是归纳得来的，要么是演绎得来的，要么是逻辑得来的。他启发了一代又一代的思想家将头脑中的逻辑推理转化为用铅笔和纸进行符号操作，并最终转化为使用计算机进行计算。

欧几里得：逻辑的论证

柏拉图学院的大门上方有一段著名的碑文：

任何不懂几何学的人都不要进入这里。

亚里士多德的学生可能会发现，在现实生活的辩论中，逻辑是有效的，但赢得辩论并不一定等于坚持真理。如果有不言自明的真理被称为公理，被直觉所选择和认同，从直觉中可以根据逻辑推理推导出更多的真理呢？欧几里得证明了已知的几何知识可以用亚里士多德的逻辑系统地解释在他的《几何原本》中。他不仅建立了几何学科，而且论证了从逻辑推理发展知识的框架。

一方面，欧几里得成功地证明了逻辑可以用来证明当时所有已知的几何真理。另一方面，通过对之前发现的所有真理的逻辑组织，他也反映了直觉的光辉，而直觉的结果是“合乎逻辑的”。这种数学发展的逻辑框架后来遇到了障碍。首先，这些公理并不总是与现实相符。例如，人们发现，欧几里得几何的公理不适用于宇宙尺度上的物理空间，根据阿尔伯特·爱因斯坦的广义相对论，在宇宙尺度上，空间被引力弯曲。其次，数学家们会发现自己被自我参照扼杀了。

莱布尼茨：逻辑即计算

比亚里士多德和欧几里得晚两千年的德国学者戈特弗里德·威廉·莱布尼茨是亚里士多德逻辑的狂热粉丝，他与牛顿共同发明了微积分。在莱布尼茨的时代，通过在代数表达式中用符号代替数字来计算数学的方法已经成熟。我们不再需要列出一个变化量的每一个数字，例如移动物体的距离，而可以用代数表达式来表示。

莱布尼茨考虑了从不同距离求速度和或从不同速度求距离的问题。为了计算任意时刻的速度，我们需要用无穷小的距离变化量除以无穷小的时间变化量。距离也是一样，我们需要累积每一个无穷小的距离变化量用速度乘以无穷小的时间变化量。第一种计算称为微分，第二种计算称为积分。在任何一种情况下，我们都需要使用一种叫做极限过程的方法来确定无穷小量任意接近于零（但不是零）时的精确表达式。

莱布尼茨的微分和积分符号

上面两个方程的左边分别是微分和积分的莱布尼茨符号。无限小的概念（即某物几乎为零，但不是零），后来被一个更严格的定义所取代。莱布尼茨展示了一个很好的例子，说明直觉如何作为一个探索者去拓展知识的前沿。

莱布尼茨发现，他的微分符号和积分符号不同于其他代表任意量的符号，因为它们有特殊的意义，发挥了强大的作用。这一发现使他产生了一组符号或“字母表”的想法，以及由此产生的一种语言，来代表亚里士多德的逻辑。他设想用新的逻辑演算把逻辑推理变成计算。

布尔：逻辑作为代数

乔治·布尔，一位英国数学家，他发现逻辑可以被表示为一种叫做布尔代数的特殊代数。他用代数变量代替了亚里士多德用来表示逻辑命题的变量。布尔变量只接受0和1作为其值，1代表TRUE，0代表FALSE。同样，代数运算“加法”和“乘法”分别代表逻辑上的“或”和“与”。布尔变量x指的是介词或类，我们有x=x，x+1=1。以“人皆有一死”为例，如果用x代表所有的人，用y代表终有一死，则上面这句话可以表示为xy=x。布尔代数使逻辑成为数学的一个分支，向实现莱布尼茨的“逻辑即计算”的梦想迈进了一步。今天，布尔代数从根本上支撑着现代计算机的运行。

弗雷格：地基上的裂缝

德国数学家戈特洛布·弗雷格（Gottlob Frege，1848-1925）没有把逻辑作为数学的一个分支，而是选择了相反的方法，把数学变成了逻辑的不同分支，他认为这比数学更基本。因此，他用一种复杂的符号语言来定义逻辑而不需要数学。有了弗雷格的符号，数学家在他那个时代使用的所有逻辑推理都可以用符号串来表示，没有歧义。例如，下面的推理：

所有的狗都是哺乳动物因此，狗的尾巴就是哺乳动物的尾巴

可以表示为：

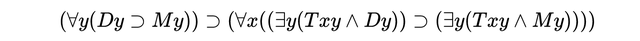
在现代一阶逻辑中，D、M、T分别表示“是一只狗”、“是一只哺乳动物”、“是……的尾巴”。读者会发现推理的符号版本更难理解。关键在于，通过将任何逻辑推理表示为符号语言中的语法操作，可以通过某种“机制”来检查其有效性。弗雷格从字面上建立了元数学，其中数学证明本身可以研究。

弗雷格试图重建算术，或者说数论，他说：为了避免自我引用，公理基于逻辑和集合的概念。

在从公理中定义数字之前，不涉及数字。

弗雷格认为集合的概念比数的概念更明显，数字被定义为集合的某一性质。你可能会想说，这个称为集合的“基数”的特定属性就是集合中成员的“数量”。但是请记住，“数字”还没有被定义。我们能说的是，如果你能找到两个集合中的元素之间的一一对应，那么它们具有相同的基数。你从之前的经验中学到的关于数字的观点不能在弗雷格的数论中计算。

弗雷格的计划是，在证明了所有已知的数论的真理都可以从他的公理和逻辑规则中派生出来之后，所有数学分支都可以在逻辑基础上重新建立起来。在遭到致命打击之前，他的野心几乎成功了。说谎者的悖论杀死了诺曼。同样，一个自我参照的悖论终结了弗雷格的数学抱负。伯特兰·罗素是英国的数学家，在弗雷格即将出版他最后一本也是最伟大的逻辑著作之前，他给弗雷格写了一封信。在信中，罗素提出了一个用弗雷格自己的符号语言表达的场景：如果一个集合是不属于它自己的所有集合的集合，那么这个集合是否属于它自己？

这种情况被证明是一种悖论。任何一个答案都会导致矛盾。弗雷格认为这一悖论是他计划建立的数学基础上的一个裂缝。弗雷格总想摆脱他那不可靠的直觉，这使他感到震惊，他绝望了，放弃了他的计划。

       出处:https://mbd.baidu.com/newspage/data/landingsuper?context=%7B%22nid%22%3A%22news_8868774820722993665%22%7D&n_type=1&p_from=4